本文引用洛谷图床图片可能无法显示,请复制链接至新标签页查看
树可以用来表示物种之间的进化关系。一棵“进化树”是一个带边权的树,其叶节点表示一个物种,两个叶节点之间的距离表示两个物种的差异。现在,一个重要的问题是,根据物种之间的距离,重构相应的“进化树”。
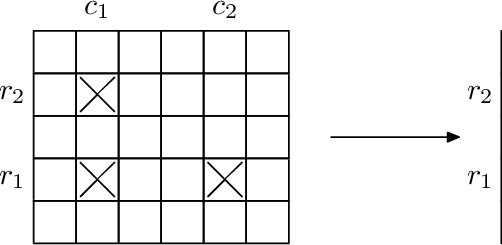
令N={1..n},用一个N上的矩阵M来定义树T。其中,矩阵M满足:对于任意的i,j,k,有M[i,j] + M[j,k] >= M[i,k]。树T满足:
1.叶节点属于集合N;
2.边权均为非负整数;
3.dT(i,j)=M[i,j],其中dT(i,j)表示树上i到j的最短路径长度。
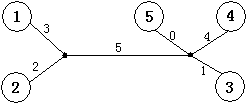
如下图,矩阵M描述了一棵树。

树的重量是指树上所有边权之和。对于任意给出的合法矩阵M,它所能表示树的重量是惟一确定的,不可能找到两棵不同重量的树,它们都符合矩阵M。你的任务就是,根据给出的矩阵M,计算M所表示树的重量。下图是上面给出的矩阵M所能表示的一棵树,这棵树的总重量为15。
非常巧妙的一道构造题.
题面指出 $对于任意的i,j,k 有M[i,j] + M[j,k] \geq M[i,k]$
那么很显然$M$描述的是两点之间的最短路了,也就是$M[i,j]=M[i,lca(i,j)]+M[j,lca(i,j)]$
我们取出一个叶子节点$a$,将它作为树根.
接下来我们逐个将叶子加入这颗树里.这个叶子一定会产生一个新枝,我们把这个叶子产生的枝加入答案$ans$
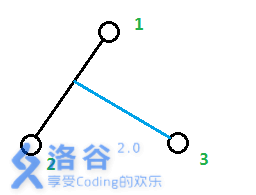
对于第二个叶子$b$,显然它只能直接和$a$连一条边,$ans=M[a,b]$
对于第三个叶子$c$,显然它只能加入链$[a,b]$中,根据$M$的信息我们可以算出$c$产生的枝长度$L$为$(M[a,c]+M[b,c]-M[a,b])/2$,将这个数字加入$ans$
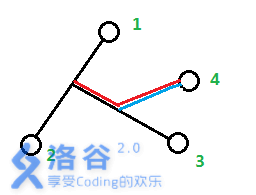
对于第四个叶子$d$,事情就没有这么简单了.它有可能加入链$[a,b]$,分枝长度$L_1$;也有可能加入链$[a,c]$,分枝长度$L_2$.我们分类讨论不同情况:
- 分支点位于$[a,lca(b,c)]$,则$L_1=L_2$
- 分支点位于$[lca(b,c),b]$,则$L_1$为$d$到$lca(b,d)$的距离;$L_2$为$d$到$lca(c,d)即lca(b,c)$的距离.显然$L_1<L_2$.如果我们认为$L$为$L_2$,那么$lca(b,d)到lca(b,c)$的这一段距离就会重复计算(我们在加入$b$的时候就把这一段加入$ans$了).所以$L$为$L_1$
- 分支点位于$[lca(b,c),c]$的时候情形同上
综上,对于第四个节点,$L=\min(L_1,L_2)$
……
推广到第$n$个节点,$L=\min{L_i}$
图片引自TsReaper的博客
代码如下
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <algorithm>
#include <string>
#include <cstring>
#include <cmath>
#define LL int
using namespace std;
LL map_[100][100],len[100],n;
int main(){
while (1){
scanf("%d",&n);
if (n == 0)
break;
else {
memset(map_,0,sizeof(map_));
memset(len,0x3f,sizeof(len));
for (LL i = 1;i <= n;++ i){
for (LL j = 1 + i;j <= n;++ j){
scanf("%d",&map_[i][j]);
map_[j][i] = map_[i][j];
}
}
}
LL ans = len[2] = map_[1][2];
for (LL i = 3;i <= n;++ i){
for (LL j = 2;j < i;++ j){
len[i] = min(len[i],(map_[i][j] + map_[i][1] - map_[1][j]) >> 1);
}
ans += len[i];
}
printf("%d\n",ans);
}
return 0;
}文结