本文采用知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议进行许可
void Tarjan(int u){
//...
if (dfn[v]){
low[u] = min(low[u], dfn[v]);
}
else{
Tarjan(v);
low[u] = min(low[u], low[v]);
}
//...
}前两天, 学弟hjk问了我这么一个问题:为什么在Tarjan中第4行代码不能写成这样
low[u] = min(low[u], low[v]);看着他求知的面庞, 我不禁想起了曾经young的自己, 同样向自己提出过这个问题..
于是我打算写篇文章来讲讲这个
这个问题并不奇怪. 因为在缩点板子题中, 显然点$u$和$low[u]$和$low[low[u]]$祖孙三代所表示的三个点最后会合并成同一个点, 那为什么不直接把$u$的$low$值设定成最远的祖父呢?
于是我尝试把这样修改的代码交上去, 很顺利, 它a过了. 但是我把它交到了割点板子题上, 它就wa得很惨.
所以这是怎么回事?为什么这种写法可以过缩点不能过割点?缩点和割点有什么区别?
点双和边双的区别
我copy一下有关点双连通分量和边双连通分量的定义
点连通度
一张图的点连通度的大小等于最小点割集的大小。
边连通度
一张图的边连通度的大小等于最小边割集的大小。
点双连通分量
点连通度大于等于$2$的分量
边双连通分量
边连通度大于等于$2$的分量
换句话说:
点双上任意删去一个点 剩下的图形依然连通.
边双上任意删去一个边 剩下的图形依然连通.
再看看缩点问题: 它实质上就是求边双. 一个边双可以缩成一个点, 缩完点之后的图形中每一条边都是割边.
于是要研究缩点和割点的区别, 就是研究点双和边双的区别. 当燃啦, 从定义上看两者就不一样.
那我能不能整个图形 它是个边双而不是点双?
这个图形不难构造, 它长这个样子
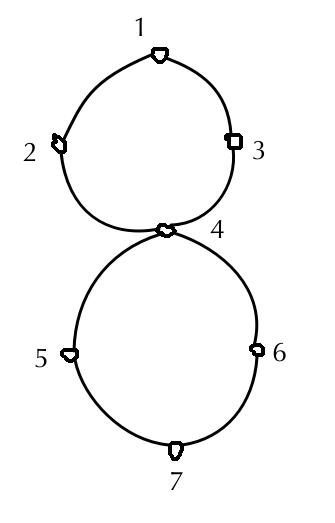
嗯 这个图中${1,2,3,4}$和${4,5,6,7}$这两个分量, 它们就是个普通的环, 所以既是点双, 又是边双.
如果两个分量由一个点$5$连接, 通过这个点 ${1,2,3,4,5,6,7}$连接成了一个大的边双, 但是它并不是个点双, 因为这个连接点$5$本身就成了那个割点.
更普通地说, 如果两个边双之间有至少一个点连接两者, 那么就可以合并成一个大的边双; 如果两个点双之间有至少两个点连接两者, 那么就可一合并成一个大的点双. 但如果有且只有一个点连接两个点双, 情况就会变成: 两者形成了一个大的边双, 但这个边双并不是点双.
我不清楚这个图有没有名字, 总之我管它叫糖葫芦图

啊放错图了. 应该是这个

言归正传
为什么用$low[v]$更新$low[u]$的写法能过缩点不能过割点? 还是看这张图

设$1$是出发点
如果依照$dfn[v]$来更新$low[u]$, 那么这张图跑一遍Tarjan会得到$low[4]=1,low[7]=dfn[4]$, 也就是说该算法会得到”$1$和$4$在一个连通分量中, $4$和$7$在一个连通分量中”. 不论我们所求是边双还是点双, 这种说法都是没错的.
但如果如果依照$low[v]$来更新$low[u]$, 那么这张图跑一遍Tarjan会得到$low[7]=low[4]=1$, 也就是说该算法会得到”$1$和$4$和$7$在一个连通分量中”, 但事实上它们三个在同一个边双中, 却不是在同一个点双中, 所以求缩点时这种算法是正确的, 求割点时就是错误的.
综上所述, 之所以这种写法在割点问题和缩点问题中的表现不同, 原因就在于点双和边双的传递性不同.
文结于CSP-J/S2019day1.
