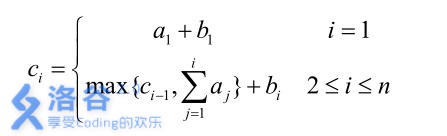我们设第 i 位大臣左手上的正整数为 ai,右手上的正整数为 bi,则第 i 位大臣获得的奖金数目为 ci可以表达为:
吝啬的皇后并不希望太多的奖金被发给大臣,所以她想请你来重新安排一下队伍的顺序,使得获得奖金最多的大臣,所获奖金数目尽可能的少。
注意:重新安排队伍并不意味着一定要打乱顺序,我们允许不改变任何一位大臣的位置。
应悠娴之邀写的一篇题解
显然我们发现,数列$c$是一个递增数列,”获得奖金最多的大臣”实际上就是最后一位大臣.
设$a_0=b_0=0$,则第$i(i\geq 1)$位大臣获得奖金$f_1$
$$
=max(c_{i-1},\sum_{j=1}^i a_j)+b_i
$$
$$
=max(max(c_{i-2},\sum_{j=1}^{i-1}a_j)+b_{i-1},\sum_{j=1}^{i}a_j)+b_i
$$
$\sum_{i=m}^{n}a_i$意为数列$a$中从第$m$项到第$n$项的累和
若我们交换第$i$和$i-1$两位大臣的位置,则当前后面这位大臣(即原先第$i-1$位)所获奖金$f_2$
$$
=max(max(c_{i-2},\sum_{j=1}^{i-2}a_j+a_i)+b_i,\sum_{j=1}^i a_j)+b_{i-1}
$$
假定交换两人之前的排列方式是更优的,也就是说
$$
f_1<f_2
$$
展开得
$$
max(max(c_{i-2},\sum_{j=1}^{i-1}a_j)+b_{i-1},\sum_{j=1}^{i}a_j)+b_i<max(max(c_{i-2},\sum_{j=1}^{i-2}a_j+a_i)+b_i,\sum_{j=1}^i a_j)+b_{i-1}
$$
再展开得
$$
max(c_{i-2}+b_{i-1}+b_{i},\sum_{j=1}^{i-1}a_j+b_{i-1}+b_i,\sum_{j=1}^ia_j+b_i)<max(c_{i-2}+b_i+b_{i-1},\sum_{j=1}^{i-2}a_j+a_i+b_i+b_{i-1},\sum_{j=1}^{i}a_j+b_{i-1})
$$
容易证明,$max(a,b)<max(a,c)$等价于$b<c$
原不等式两边同时消去$c_{i-2}+b_{i-1}+b_{i}$
$$
max(\sum_{j=1}^{i-1}a_j+b_{i-1}+b_i,\sum_{j=1}^ia_j+b_i)<max(\sum_{j=1}^{i-2}a_j+a_i+b_i+b_{i-1},\sum_{j=1}^{i}a_j+b_{i-1})
$$
两边同时减去$\sum_{j=1}^ia_j$
$$
max(-a_i+b_{i-1}+b_i,b_i)<max(-a_{i-1}+b_i+b_{i-1},b_{i-1})
$$
两边同时减去$(b_i+b_{i-1})$
$$
max(-a_i,-b_{i-1})<max(-a_{i-1},-b_i)
$$
去负号
$$
min(a_i,b_{i-1})>min(a_{i-1},b_i)
$$
至此,我们得到了一个形式较为简单的,只与相邻两项有关的不等式.根据这个不等式进行排序即可.
完整代码如下:
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cmath>
#include <string>
#include <algorithm>
#define LL long long
using namespace std;
LL n;
struct pwp{
LL a,b;
bool operator < (const pwp &qwq)const{
return min(qwq.a,b) > min(a,qwq.b);
}
}arr[40000];
//Both overloading operator function and defining a compare function are correct
bool cmp(const pwp &al,const pwp &be){
//"al" is short for "alpha","be" is short for "beta"
return min(be.a,al.b) > min(al.a,be.b);
}
int main (){
LL T;
cin >> T;
arr[0] = (pwp){0,0};
while(T --){
LL ans = 0,sum_ = 0;
cin >> n;
for (LL i = 1;i <= n;++ i)
scanf("%lld%lld",&arr[i].a,&arr[i].b);
sort(arr + 1,arr + 1 + n);
for (LL i = 1;i <= n;++ i){
sum_ += arr[i].a;
ans = max(ans,sum_) + arr[i].b;
}
printf("%lld\n",ans);
}
return 0;
}考虑另一点:原式为什么不是$f_1\leq f_2$?
- 比较函数
cmp或<定义的是严格小于,不能用小于等于去定义它们- $max(a,b)\leq max(a,c)$不等价于$b\leq c$
求解这类”求某方案,使某值最大/小”的贪心问题可以考虑假定一个最佳方案,然后对该方案进行略微改动,列不等式,观察不等式得到贪心策略.
这种方法称为”微调法”(似乎?),在很多贪心问题上都很实用.
文结.