Innopolis University scientists continue to investigate the periodic table. There are n·m known elements and they form a periodic table: a rectangle with n rows and m columns. Each element can be described by its coordinates (r, c) (1 ≤ r ≤ n, 1 ≤ c ≤ m) in the table.
Recently scientists discovered that for every four different elements in this table that form a rectangle with sides parallel to the sides of the table, if they have samples of three of the four elements, they can produce a sample of the fourth element using nuclear fusion. So if we have elements in positions (r1, c1), (r1, c2), (r2, c1), where r1 ≠ r2 and c1 ≠ c2, then we can produce element (r2, c2).
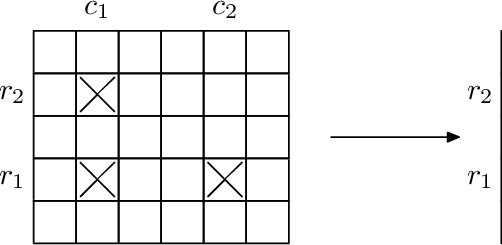
Samples used in fusion are not wasted and can be used again in future fusions. Newly crafted elements also can be used in future fusions.
Innopolis University scientists already have samples of q elements. They want to obtain samples of all n·m elements. To achieve that, they will purchase some samples from other laboratories and then produce all remaining elements using an arbitrary number of nuclear fusions in some order. Help them to find the minimal number of elements they need to purchase.
先下一个定义:
- 联通矩阵:若有一个元素组成的集合,集合内任意一个元素都已存在或可以由同集合已存在的元素合成.显然这个集合最大时是一个(不一定连续的)矩阵形状,称联通矩阵
观察联通矩阵的性质
- 若有两联通矩阵A,B.其中分别有两元素a,b.这两个元素在同一行(或同一列)时,两矩阵可以合成一个更大联通矩阵C.C的左边界为A,B左边界较小的一个,C的右边界为A,B右边界较大的一个.上下边界同理
- 若整张地图共有k个联通矩阵(当然它们两两之间无法合并),则只需添加k-1个元素就可以使整张地图联通
接着逐行模拟合并联通矩阵的过程
- 考虑前i-1行,若有一个联通矩阵A,包含$J_1,J_2,…,J_k$几个列.第i行存在任意一个元素$(i,J_t),J_t属于J$,则所有$(i,J_1),(i,J_2),…,(i,J_k)$加入矩阵A
- 考虑前i-1行,若有两个联通矩阵$A={J_{A1},J_{A2},…,J_{Ak}}$,$B={J_{B1},J_{B2},…,J_{Bk}}$,第i行存在两元素$(i,J_{At})$,$(i,J_{Bt})$,$J_{At}属于J_A,J_{Bt}属于J_B$,则将AB合并为一个矩阵
- 当然以本题规模无法存下整个矩阵.由于我们是逐行枚举的,所以只要存储矩阵中的所有列就可以代表一个包含以上所有行与这些列的交点的联通矩阵了
- 值得注意的是:用列来表示不会忽略空列,但是会忽略空行.因此应当加上所有空行的数量(显然在一个空行上任意添加一个元素就可以将整个行加入矩阵)
- 显然以上说的这些应该用并查集维护
以下是代码:
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <string>
#include <cmath>
#include <algorithm>
#define llint long long
using namespace std;
struct coo{
int x,y;
bool operator < (const coo &be)const{
if (x != be.x) return x < be.x;
else return y < be.y;
}
}arr[400000];
//set
int fa[400000];
int set_(int k){
if (k == fa[k]) return k;
else return fa[k] = set_(fa[k]);
}
int merge(int k,int l){
fa[set_(k)] = set_(l);
return set_(k);
}
int main (){
int n,m,k,ans = 0;
cin >> n >> m >> k;
for (int i = 1;i <= k;++ i){
scanf("%d%d",&arr[i].x,&arr[i].y);
}
sort(arr + 1,arr + 1 + k);
for (int i = 1;i <= m;++ i)
fa[i] = i;
int p = 0,cnt = 0;
bool ifcnt = 0;
for (int i = 1;i <= n;++ i){
int f = 0;
while (++p <= k && arr[p].x == i){
ifcnt = 1;
int &y = arr[p].y;
if (!f) f = set_(y);
else merge(y,f);
}
if (!ifcnt) ++ cnt;
ifcnt = 0;
p --;
}
int f = set_(1);
for (int i = 2;i <= m;++ i){
if (set_(f) != set_(i)) {
++ ans;
f = merge(f,set_(i));
}
}
cout << ans + cnt;
return 0;
}以上.